Definición de la derivada
El método de Fermat para calcular la pendiente fue desarrollado durante 1630 y,
aunque no es riguroso, es tan exacto como el utilizado posteriormente por Newton
y Leibniz, sin utilizar el concepto de límite. Con una misteriosa , Fermat
desarrollo un método para hallar tangentes a curvas planas. El método de Fermat
fue fuertemente criticado por sus contemporáneos. Ellos objetaban obre la
misteriosa . Dividir por significaba que era diferente a cero, pero eliminarla
significaba tratarla como si fuera igual a cero, lo cual era inamisible.

Pero la
misteriosa después se convirtió en la diferencial de x (dx) o en las cantidades
infinitamente pequeñas de Leibniz. De ahí que en libros de historia de las
matemáticas se afirma que: Aunque la lógica de la exposición de Fermat deja
mucho que desear. Leibniz afirmo “ no se aproxima a cero. En vez de eso, el
ultimo valor de no es cero sino una “cantidad infinitamente pequeña” una
“diferencial” llamada ”, y de manera similar tiene un valor último infinitamente
pequeño llamado. El cociente real de estas diferenciales infinitamente pequeñas
es nuevamente un numero ordinario llamado derivada f´(x)= dy/dx En este sentido
ƒ' (x), representa a la derivada de la función ƒ en un punto de la nueva función
ƒ', en el cual dicha función es derivable;
Reglas para determinar la derivada de una función:
Si está definida sobre un intervalo abierto , entonces para cada dos puntos
distintos sea f una función real definida en un intervalo abierto , y supongamos
que, diremos que f es diferenciable en c siempre que el límite existe. El
limite, designado por se llama derivada de f en y podemos considerar el cociente
de diferencias llamado cociente incremental. Este método de calcular límites
define una nueva función, cuyo dominio está formado por aquellos puntos de en
los que se llama primera derivada de f. La n es derivada de designada por fn,”.
Además, la derivada de una función es , límite con el que se calcula la derivada
de una función por definición; sin embargo, las dificultades didácticas están
vinculadas con el rechazo operacional que permite el paso al límite, la noción
de función y continuidad, así como los obstáculos geométricos, lógicos y
simbólicos (Sierpinska, 1994). En la fórmula, x es el punto en el que la
variable toma el valor de x. Así mismo, h es cualquier número. Este luego se
igualará a cero pues, como vemos en la imagen superior, debemos calcular el
límite de la función cuando h se acerca a cero.
La derivada es una función
matemática que se define como la tasa de cambio de una variable respecto a otra.
Es decir, en qué porcentaje aumenta o disminuye una variable cuando otra también
se ha incrementado o disminuido. Debemos precisar que el límite de una función
se define como la tendencia de esta (a qué valor se aproxima) cuando uno de sus
parámetros (en este caso h) se acerca a un valor determinado.
Ejemplo:
En el proceso del método cuatro pasos para derivar, h es el incremento en el
eje, de manera indistinta se trabaja con h o su equivalente; hecha la aclaración
y con la finalidad de que el cálculo de la derivada por definición se facilite,
tal como sugiere Tan (2000):
(1) "Se calcula ƒ(x+h)
(2) Se formula y calcula la
diferencia ƒ(x+h)-ƒ(x)
(3) Se formula y calcula el cociente
(4) Se reemplaza y
calcula.
Reglas para determinar la derivada de una función:
El procedimiento para obtener la derivada de una función por el método de los cuatro pasos es directo; sin embargo, hay funciones donde realmente se llega a complicar el desarrollo algebraico y la determinación de los límites. Previamente conociste que es posible encontrar funciones de tipo algebraico, trigonométrico, exponencial y logarítmico, entre muchas otras.
Por ello, se han obtenido reglas que relacionan una función “tipo” con su derivada; las mismas se han obtenido a través de la aplicación del método de los cuatro pasos a ecuaciones de carácter general para su clase.
Los elementos para contestar esta pregunta sin mucho problema ya se tienen a la mano; uno es la derivación, la cual puede informar sobre la manera en que sucede esto. El hecho de derivar una función sucesivamente se denomina derivación de orden superior; el algoritmo para realizarla es el mismo y la notación de esta acción es similar. En el estilo de Lagrange es fácil indicarla, ya que es recurrente en su escritura:
y´ (primera derivada)
y´´ (segunda derivada)
yn (enésima derivada)
El interés de realizar derivaciones de orden superior se debe a que la derivada es una herramienta matemática muy versátil para evaluar el cambio en una función, y su aplicación depende mucho de las interpretaciones que se hagan de sus resultados.
1. Obtener la derivada de la función bajo análisis, igualar dicha ecuación a cero y obtener las soluciones para esa condición.
2. Evaluar para valores cercanos antes y después de esos puntos donde se anula la derivada.
3. Obtener, si se presentan, los cambios de signo asociados a las tangentes evaluadas.
4. Se presenta un máximo si la variación de signos alrededor del valor que se anula se da de esta forma: positivo-cero-negativo.
5. Se presenta un mínimo si la variación de signos alrededor del punto que se anula se da de esta manera: negativo-cero-positivo.
Referencias Paragua Morales, M., Pasquel Loarte, L., Paragua Macuri, C. A.,
Paragua Macuri, M. G., & Cajas Bravo, T. V. (2018). Método cuatro pasos y el
aprendizaje de la derivada por definición. Comuni@ cción, 9(1), 48-55. Robayo,
Y. A. L. (2011). Desarrollo del concepto de la derivada sin la noción del límite
(Doctoral dissertation, Universidad Nacional de Colombia). Sánchez-Matamoros,
G., García, M., & Llinares, S. (2008). La comprensión de la derivada como
objeto de investigación en didáctica de la matemática. Revista latinoamericana
de investigación en matemática educativa, 11(2), 267-296.
https://programas.cuaed.unam.mx/repositorio/moodle/pluginfile.php/1146/mod_resource/content/1/contenido/index.html
https://es.khanacademy.org/math/differential-calculus/dc-diff-intro
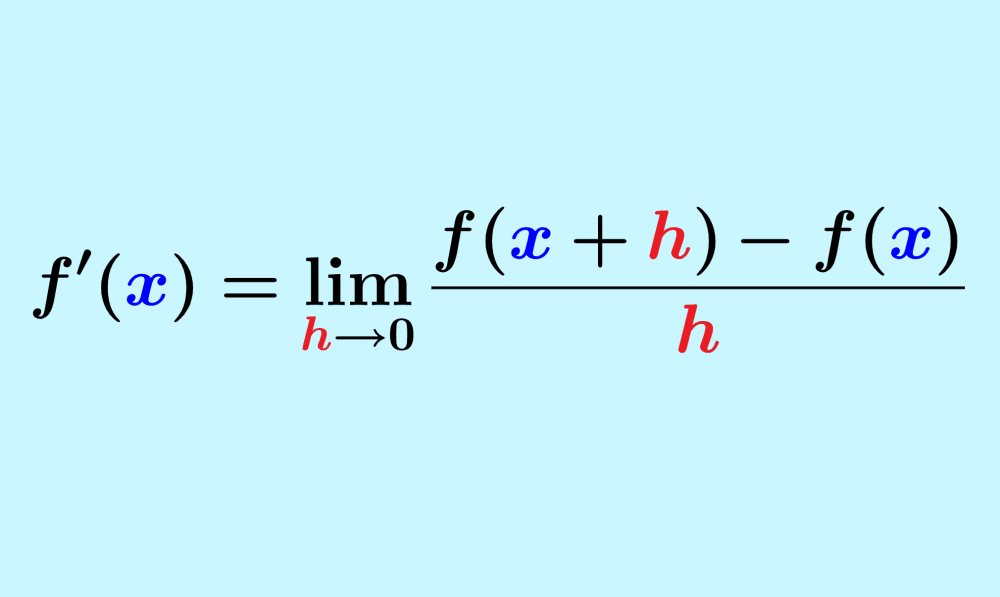



Comentarios
Publicar un comentario