Integración por potencias por funciones trigonométricas
Integración por potencias por funciones trigonométricas
La primera regla se refiere a las integrales de las funciones trigonométricas básicas: seno, coseno y tangente. Estas integrales tienen fórmulas específicas que se utilizan para simplificar los cálculos. A continuación, se muestran las fórmulas básicas de integración trigonométrica:
– Integral del seno: ∫sin(x)dx = -cos(x) + C
– Integral del coseno: ∫cos(x)dx = sen(x) + C
– Integral de la tangente: ∫tan(x)dx = -ln|cos(x)| + C
Estas fórmulas se utilizan para encontrar la integral de una función trigonométrica específica. Es importante recordar que siempre debes agregar una constante de integración (C) al final de la integral.
– Integral del seno: ∫sin(x)dx = -cos(x) + C
– Integral del coseno: ∫cos(x)dx = sen(x) + C
– Integral de la tangente: ∫tan(x)dx = -ln|cos(x)| + C
Estas fórmulas se utilizan para encontrar la integral de una función trigonométrica específica. Es importante recordar que siempre debes agregar una constante de integración (C) al final de la integral.
La segunda regla se aplica a las integrales de funciones trigonométricas compuestas, donde una función trigonométrica está dentro de otra función. Para integrar estas funciones, se utilizan sustituciones trigonométricas. A continuación, se muestra un ejemplo de una sustitución trigonométrica común:
– Integral de secante al cuadrado: ∫sec^2(x)dx = tan(x) + C
En este caso, se utiliza la sustitución trigonométrica u = sen(x) + cos(x) para simplificar la integral y encontrar su solución.
– Integral de secante al cuadrado: ∫sec^2(x)dx = tan(x) + C
En este caso, se utiliza la sustitución trigonométrica u = sen(x) + cos(x) para simplificar la integral y encontrar su solución.
La integración de potencias de funciones trigonométricas implica la manipulación algebraica de funciones trigonométricas elevadas a una potencia. Estas funciones pueden incluir seno, coseno, tangente, cotangente, secante y cosecante. Al integrar estas funciones, es importante recordar las fórmulas trigonométricas y las propiedades de las potencias.Para integrar ∫cosʲxsenᴷxdx, use las siguientes estrategias:
Si k es impar, reescriba senᴷx = senᴷ⁻¹xsen²x y use la identidad sen²x = 1 − cos²x para reescribir senᴷ⁻¹x en términos de cosx. Integrar usando la sustitución u = cosx. Esta sustitución hace du = −senxdx.
Si j es impar, reescriba cosʲx = cosʲ⁻¹xcosx y use la identidad cos²x = 1 − sin²x para reescribir cosʲ⁻¹x en términos de senx. Integrar usando la sustitución u = senx. Esta sustitución hace du = cosxdx. (Nota: si tanto j como k son impares, se puede usar la estrategia 1 o la estrategia 2).
Si tanto j como k son pares, use sen²x = (1/2) – (1/2) cos(2x) y cos²x = (1/2) + (1/2)cos (2x). Después de aplicar estas fórmulas, simplifique y vuelva a aplicar las estrategias 1 a 3 según corresponda.
Si k es impar, reescriba senᴷx = senᴷ⁻¹xsen²x y use la identidad sen²x = 1 − cos²x para reescribir senᴷ⁻¹x en términos de cosx. Integrar usando la sustitución u = cosx. Esta sustitución hace du = −senxdx.
Si j es impar, reescriba cosʲx = cosʲ⁻¹xcosx y use la identidad cos²x = 1 − sin²x para reescribir cosʲ⁻¹x en términos de senx. Integrar usando la sustitución u = senx. Esta sustitución hace du = cosxdx. (Nota: si tanto j como k son impares, se puede usar la estrategia 1 o la estrategia 2).
Si tanto j como k son pares, use sen²x = (1/2) – (1/2) cos(2x) y cos²x = (1/2) + (1/2)cos (2x). Después de aplicar estas fórmulas, simplifique y vuelva a aplicar las estrategias 1 a 3 según corresponda.
Fórmulas de reducción
La evaluación de ∫secⁿxdx para valores de n donde n es impar requiere integración por partes. Además, también debemos conocer el valor de ∫secⁿ⁻²xdx para evaluar ∫secⁿxdx. La evaluación de ∫tanⁿxdx también requiere poder integrar ∫tanⁿ⁻²xdx. Para facilitar el proceso, podemos derivar y aplicar las siguientes fórmulas de reducción de potencia. Estas reglas nos permiten reemplazar la integral de una potencia de secx o tanx con la integral de una potencia menor de secx o tanx.
La evaluación de ∫secⁿxdx para valores de n donde n es impar requiere integración por partes. Además, también debemos conocer el valor de ∫secⁿ⁻²xdx para evaluar ∫secⁿxdx. La evaluación de ∫tanⁿxdx también requiere poder integrar ∫tanⁿ⁻²xdx. Para facilitar el proceso, podemos derivar y aplicar las siguientes fórmulas de reducción de potencia. Estas reglas nos permiten reemplazar la integral de una potencia de secx o tanx con la integral de una potencia menor de secx o tanx.
Ejemplo:
Evaluar ∫sen²xdx.
Solución:
Para evaluar esta integral, usemos la identidad trigonométrica sen²x = 1/2 − (1/2)cos(2x). Así,
El proceso general para integrar productos de potencias de senx y cosx se resume en el siguiente conjunto de pautas.
Evaluar ∫sen²xdx.
Solución:
Para evaluar esta integral, usemos la identidad trigonométrica sen²x = 1/2 − (1/2)cos(2x). Así,
El proceso general para integrar productos de potencias de senx y cosx se resume en el siguiente conjunto de pautas.A consideración: Para la mayoría de las integrales de productos y potencias de tanx y secx, reescribimos la expresión que deseamos integrar como la suma o diferencia de integrales de la forma ∫tanʲxsec²xdx o ∫secʲxtanxdx.
Para convertir esta integral en integrales de la forma ∫cosʲx senxdx, reescribe sen³x = sen²xsenx y realiza la sustitución sen²x = 1 − cos²x. Así,
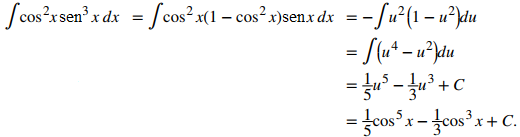En el siguiente ejemplo, vemos la estrategia que debe aplicarse cuando solo hay potencias pares de senx y cosx. Para integrales de este tipo, las identidades
Referencias:
Integrales trigonométricas | Calculo21
Integrales trigonométricas | Calculo21
Comentarios
Publicar un comentario