Integración por partes
Integración por partes

Ejercicio de fácil memorización
Un Día Vi Una Vaca sin cola Vestida De Uniforme
o también
un día vi una vaca sin cola vestida de unicornio
Método:
- El integrando debe ser un producto de dos factores (si no lo es, podemos transformarlo para que lo sea).
- Uno de los factores será y el otro será .
- Se calcula derivando y se calcula integrando .
- Se aplica la fórmula.
Paso 1: Elección Estratégica de “u” y “dv”
La elección adecuada de las funciones “u” y “dv” es un primer paso crucial. Generalmente, seleccionamos “u” de tal manera que su derivada “du” sea más simple que “u” en sí mismo, y elegimos “dv” de modo que su integral “v” sea más simple que “dv”. Esta elección estratégica se basa en la regla mnemotécnica “LIATE,” que prioriza las siguientes funciones:
- Logaritmos (logaritmos y funciones inversas) sin-1(x), cos-1(x), tan-1(x)
- Inversas trigonométricas ln (x), log (x)
- Algebraicas (polinomios y funciones algebraicas) x2, x3
- Trigonométricas sin(x), cos(x), tan (x)
- Exponenciales ex, 3x
Integrales cíclicas:
Ejemplo 1 de Integración por Partes Paso a Paso
La exponencial no cambia al derivar ni al integrar, así que no importa si le asignamos ó .
No ocurre lo mismo con :
- Al derivar se reduce su exponente en 1 y pasa a ser una constante.
- Al integrar aumenta su exponente en 1.
Por tanto, la elección más apropiada es y .
Derivamos para calcular :
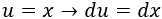
Integramos para calcular :
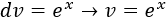
Aplicamos la fórmula de integración por partes:
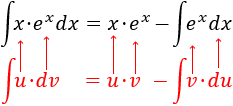
Finalmente, resolvemos la nueva integral (la de la exponencial) y añadimos la constante de integración
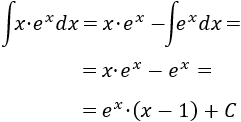
Nota: como ya hemos dicho, es importante escoger para reducir el grado del monomio al derivar. Si por el contrario hubiésemos escogido , entonces
, aumentando el grado (de 1 a 2) y complicando más la integral, pues el factor de la exponencial se mantiene igual y nos aparece la integral⋅exdxEjemplo 2 de Integración por Partes Paso a Paso
Para que este proceso sea más claro, consideremos un ejemplo práctico:
Siguiendo los pasos mencionados, calculamos esta integral paso a paso:
- u es la
es
por lo tanto:
Sustituyendo:
Es importante tener en cuenta que para poder estudiar con éxito esta materia, debes dominar perfectamente el cálculo de derivadas y las integrales inmediatas.
Ejemplo 3 de Integración por Partes Paso a Paso
Hallar la integral ∫ex x dx
Elige u y dv:
- u = ex
- dv = x
Deriva u: (ex)' = ex
Integra dv: ∫x dx = x2/2
Ahora pon todo junto:
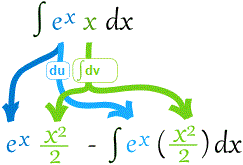


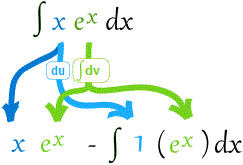
Comentarios
Publicar un comentario