Reglas de derivación

 Maria Esther Alvarez Rico                                                                                                           Oct 18th, 23

Reglas de derivación

El cálculo de la derivada de una función puede realizarse a partir de un conjunto de reglas fijas de aplicación sistemática. A la hora de derivar una función, se utilizan primero las propiedades generales de la derivación, para reducirla a una serie de funciones simples conocidas, cuyas derivadas se obtienen directamente a partir de una tabla.

Es un proceso que usa diferentes métodos para llegar a la derivada de una función; varios de ellos son los que corresponden a reglas para: funciones que se dividen entre ellas, funciones que se multiplican entre ellas o funciones compuestas.

Regla de los cuatro pasos

El proceso más general utilizado para la obtención de derivadas de funciones se denomina regla de los cuatro pasos. Dada una función f (x) continua y derivable, esta regla aplica las siguientes etapas:
Se determina: f (x + h).
Se calcula: f (x + h) - f (x).
Se obtiene el cociente incremental entre ambos términos:
Se calcula el límite de este cociente incremental cuando h tiende a cero:


Suma y diferencia de funciones

Dadas dos funciones u (x) y v (x) continuas y derivables, la derivada de la función suma (o diferencia) de las dos es igual a la suma (o diferencia) de sus derivadas.

Producto de una función por una constante

Dada una función f (x) continua y derivable y un número real l, la derivada del producto de ambos es igual al producto de la constante por la derivada de la función.

Dada una función:

Entonces la derivada será:

Producto de funciones

Dadas dos funciones continuas y derivables, la derivada del producto de las dos es igual a la derivada de la primera por la segunda, sin derivar, más la primera por la derivada de la segunda. Dada una función:

Entonces su derivada se calcula como:

Cociente de funciones

Dadas dos funciones continuas y derivables u (x) y v (x), donde la segunda es distinta de cero, la derivada del cociente de la primera por la segunda se determina con arreglo a la expresión dada a continuación.

Dada una función:


Se cumple que su derivada primera es:

Composición de funciones

Dada una función f (u) derivable con respecto a u, siendo u derivable con respecto a x, la derivada de la composición de funciones f [u(x)] con respecto a x es igual al producto de la derivada de f con respecto a u por la derivada de u con respecto a x.

Es decir, si


entonces se cumple que:

Ejemplo 1

Sea la función

Enunciamos las reglas de derivación y de la cadena y proporcionamos algunos ejemplos de su aplicación. Derivadas. Cálculo diferencial. Matemáticas.

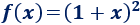
Es composición de las siguientes funciones:

Enunciamos las reglas de derivación y de la cadena y proporcionamos algunos ejemplos de su aplicación. Derivadas. Cálculo diferencial. Matemáticas.

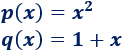
ya que

Enunciamos las reglas de derivación y de la cadena y proporcionamos algunos ejemplos de su aplicación. Derivadas. Cálculo diferencial. Matemáticas.

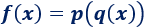
O, equivalentemente, 

�=�(�).

Las derivadas son

Enunciamos las reglas de derivación y de la cadena y proporcionamos algunos ejemplos de su aplicación. Derivadas. Cálculo diferencial. Matemáticas.

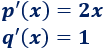
Por tanto, por la regla de la cadena,

                                         Enunciamos las reglas de derivación y de la cadena y proporcionamos algunos ejemplos de su aplicación. Derivadas. Cálculo diferencial. Matemáticas.

Enunciamos las reglas de derivación y de la cadena y proporcionamos algunos ejemplos de su aplicación. Derivadas. Cálculo diferencial. Matemáticas.

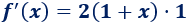
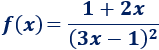
Tenemos que aplicar la regla del cociente y de la cadena (para el cuadrado):

Enunciamos las reglas de derivación y de la cadena y proporcionamos algunos ejemplos de su aplicación. Derivadas. Cálculo diferencial. Matemáticas.

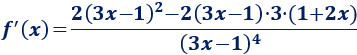
Simplificamos:

Enunciamos las reglas de derivación y de la cadena y proporcionamos algunos ejemplos de su aplicación. Derivadas. Cálculo diferencial. Matemáticas.

Enunciamos las reglas de derivación y de la cadena y proporcionamos algunos ejemplos de su aplicación. Derivadas. Cálculo diferencial. Matemáticas.

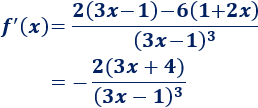
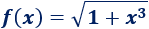
Si es necesario, se puede escribir la raíz como una potencia con exponente 

Aplicando la regla de la cadena,

Enunciamos las reglas de derivación y de la cadena y proporcionamos algunos ejemplos de su aplicación. Derivadas. Cálculo diferencial. Matemáticas.

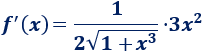
Criterio de extremos:

Si \(f\) es derivable en un extremo (máximo o mínimo local), entonces la derivada es 0 en dicho punto.

Criterio de monotonía:

Si \(f\) es derivable en \(a\):

  • Si \(f'(a)>0\), entonces \(f\) es creciente en un entorno de \(a\).

  • Si \(f'(a)< 0\), \(f\) es decreciente en un entorno de \(a\).

  • Si \(f'(a)=0\), decimos que \(a\) es un punto crítico, esto significa que \(a\) es un posible extremo (local).

Criterio de extremo (segunda derivada): Si \(a\) es un punto con \(f'(a)=0\) (es decir, \(a\) es un punto crítico) y \(f\) admite segunda derivada en \(a\):

  • Si \(f''(a)>0\), el punto \(a\) es un mínimo local.

  • Si \(f''(a)< 0\), el punto \(a\) es un máximo local.

  • Si \(f''(a)=0\), el punto \(a\) es un punto de inflexión (punto donde cambia la monotonía).


Referencias

https://www.hiru.eus/es/matematicas/reglas-de-derivacion-i
https://www.matesfacil.com/derivadas.htm
https://www.ugr.es/~rpaya/documentos/CalculoII/2012-13/Reglas.pdf
https://estudiarfisica.com/2015/07/22/demostracion-de-las-reglas-elementales-de-derivacion/
https://www.ugr.es/~rpaya/documentos/CalculoII/2013-14/Reglas.pdf
https://www.problemasyecuaciones.com/funciones/derivadas/reglas-derivacion-cadena-ejemplos-suma-resta-producto-cociente-derivadas.html
https://www.fisicalab.com/apartado/reglas-derivacion
https://www.matematicasonline.es/pdf/Temas/2BachCT/Calculo%20de%20derivadas.pdf

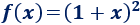
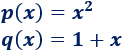
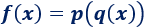
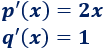
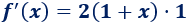
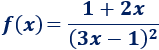
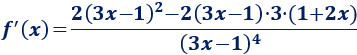
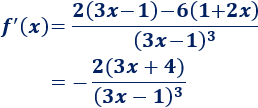
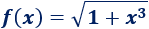
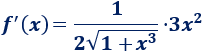
Comentarios

Publicar un comentario

Entradas populares de este blog

La antiderivada y la integral indefinidas

Imagen
Una integral se puede asimilar a una suma de infinitos términos, todos ellos de tamaño infinitesimalmente pequeño.  Por lo tanto tendrá aplicación en cualquier situación que debamos sumar fragmentos muy pequeños para hallar un todo. Por ejemplo, ya se ha dicho que las integrales se usan para hallar longitudes, áreas, volúmenes, masas, densidades. ¿Por qué se pueden usar para eso? Pues porque cada uno de esos cálculos puede pensarse como la suma de elementos de tamaño muy pequeño. Supongamos que queremos calcular un área. Podemos descomponerla en multitud de pequeños cuadraditos, de forma que el área total sería el número de cuadraditos multiplicado por el área de uno de ellos. Haciendo cuadraditos de medida cada vez más pequeña (y por tanto, aumentando su número) podríamos ajustarnos tanto como quisiéramos a cualquier tipo de contorno, de forma que los resultados obtenidos cada vez sean más exactos (es decir, más parecidos al área en cuestión). En el límite, cuando esos cuadraditos fu
Leer más

Definición de la derivada

Imagen
El método de Fermat para calcular la pendiente fue desarrollado durante 1630 y, aunque no es riguroso, es tan exacto como el utilizado posteriormente por Newton y Leibniz, sin utilizar el concepto de límite. Con una misteriosa , Fermat desarrollo un método para hallar tangentes a curvas planas. El método de Fermat fue fuertemente criticado por sus contemporáneos. Ellos objetaban obre la misteriosa . Dividir por significaba que era diferente a cero, pero eliminarla significaba tratarla como si fuera igual a cero, lo cual era inamisible. Pero la misteriosa después se convirtió en la diferencial de x (dx) o en las cantidades infinitamente pequeñas de Leibniz. De ahí que en libros de historia de las matemáticas se afirma que: Aunque la lógica de la exposición de Fermat deja mucho que desear. Leibniz afirmo “ no se aproxima a cero. En vez de eso, el ultimo valor de no es cero sino una “cantidad infinitamente pequeña” una “diferencial” llamada ”, y de manera similar tiene un valor último inf
Leer más

Método de discos y arandelas

Imagen
Método de discos Si una región del plano, se hace girar al rededor de un eje paralelo al eje , de tal forma que se genera un sólido de revolución cuyas secciones transversales perpendiculares al eje de rotación, son discos con centro en el eje de revolución. Entonces el volumen del sólido esta dado por donde es el radio del disco expresado en términos de la variable de integración. En otras palabras (palabras menos coloridas), el método del disco es el proceso de encontrar el volumen de un objeto dividiendo ese objeto en muchos cilindros / discos pequeños y luego sumando los volúmenes de estos pequeños discos.  El radio del cilindro está dado por una función f (x) y la altura es el cambio en x . Si encontramos el límite del volumen cuando el cambio en x llega a cero y el número de discos se acerca al infinito, entonces tendremos el volumen real del objeto y no solo una estimación. Este volumen es la anti-derivada del cuadrado de la función f ( x ) del punto a al punto b, multiplica
Leer más