Longitud de arco de una curva
Longitud de arco de una curva

Sea f(x) una función suave definida sobre [a, b]. Queremos calcular la longitud de la curva desde el punto (a, f (a)) hasta el punto (b, f (b)). Comenzamos usando segmentos de recta para aproximar la longitud de la curva. Para i = 0, 1, 2, …, n, sea P = {xi} una partición regular de [a, b].
Luego, para i = 1, 2, …, n, se construye un segmento de recta desde el punto (xi − 1, f(xi − 1)) hasta el punto (xi, f(xi)). Aunque parezca lógico usar segmentos de recta horizontales o verticales, queremos que nuestros segmentos de recta se aproximen a la curva lo más posible. La figura muestra esta construcción para n = 5. Podemos aproximar la longitud de una curva agregando segmentos de recta.



Video:
En esta parte del curso se consideran algunas aplicaciones de la integral definida. Para cada una es imperativo enfocar el estudio en el entendimiento del establecimiento del diferencial de la cualidad a cuantificar. Recuerde que la integral definida es el resultado de sumar una cantidad infinitamente grande de diferenciales.
El establecimiento de la integral definida consiste en dividir al todo apropiadamente esto es, de manera que para cada una de sus partes, se pueda calcular lo que se quiere calcular del todo, calcular la cualidad para una parte genérica (el diferencial de la cualidad) y sumar todas las partes. Dado que el todo se dividió en una cantidad infinitamente grande de partes, el concepto de integral definida emerge como la solución a este tipo de problemas.
En las primeras cinco aplicaciones consideradas en este libro se ejemplifica el uso del decálogo para el establecimiento de una integral definida. Este decálogo sirve como un esquema de solución para este tipo de problemas. Se espera que el lector siga aplicándolo en todos los ejemplos resueltos y en los ejercicios donde sea conveniente.
Longitud de arco
El problema de calcular la longitud de la curva se conocía en la antigüedad como la «rectificación de la curva». Este problema consiste en calcular la longitud de una parte de la gráfica de una función continua ![]() . El siguiente procedimiento es aplicable si la función es continua y diferenciable en un intervalo dado. Primero se calcula un valor aproximado de la longitud y luego, la aproximación sugiere que para obtener el valor exacto, se debe evaluar una integral definida.
. El siguiente procedimiento es aplicable si la función es continua y diferenciable en un intervalo dado. Primero se calcula un valor aproximado de la longitud y luego, la aproximación sugiere que para obtener el valor exacto, se debe evaluar una integral definida.
Cálculo aproximado de la longitud de arco
Considere la función continua y diferenciable ![]() en el intervalo
en el intervalo ![]() . Para calcular un valor aproximado de su longitud en el intervalo mencionado, siga el procedimiento que se explica a continuación.
. Para calcular un valor aproximado de su longitud en el intervalo mencionado, siga el procedimiento que se explica a continuación.
- 1. Sea «el todo» la parte de la gráfica de la función
 que inicia en el punto
que inicia en el punto  y termina en el punto
y termina en el punto  .
. - 2. Sea
 el valor exacto de la longitud de esa parte de la gráfica.
el valor exacto de la longitud de esa parte de la gráfica. - 3. Divida el intervalo
![Rendered by QuickLaTeX.com [a,b]](https://www.aprendematematicas.org.mx/wp-content/ql-cache/quicklatex.com-9c6546d13baaf33ab0e8e2033baddf08_l3.png) en un número (natural) finito
en un número (natural) finito  de subintervalos todos de igual longitud,
de subintervalos todos de igual longitud,  , de manera que:
, de manera que:Suponga que los extremos de cada subintervalo están en
 y
y  , tal que:
, tal que: - 4. Observe que a cada subintervalo
![Rendered by QuickLaTeX.com [x_{i}, x_{i+1}]](https://www.aprendematematicas.org.mx/wp-content/ql-cache/quicklatex.com-cbd37cc99e71e648230c9dc07249ec9b_l3.png) , le corresponde una parte de la gráfica de la función.
, le corresponde una parte de la gráfica de la función. - 5. Sea
 el valor exacto de la longitud de la parte de la gráfica de la función correspondiente al
el valor exacto de la longitud de la parte de la gráfica de la función correspondiente al  ésimo subintervalo.
ésimo subintervalo. - 6. La estrategia consiste en calcular un valor aproximado de la longitud
 de cada una de estas partes considerando que cada una es un segmento de recta y luego sumar todos estos valores para obtener una aproximación de la longitud de la gráfica de la función, con base en que:
de cada una de estas partes considerando que cada una es un segmento de recta y luego sumar todos estos valores para obtener una aproximación de la longitud de la gráfica de la función, con base en que: - 7. Evalúe la función
 en cada punto
en cada punto  para
para  para obtener las coordenadas de los puntos
para obtener las coordenadas de los puntos 
sobre la gráfica de la función. Observe que éstas son las coordenadas de los puntos de los extremos de cada elemento de longitud
de los extremos de cada elemento de longitud  .
.Para cada par de puntos
 y
y  , calcule la longitud
, calcule la longitud  , aplicando el teorema de Pitágoras. Este es un valor aproximado de la longitud del elemento de longitud de arco
, aplicando el teorema de Pitágoras. Este es un valor aproximado de la longitud del elemento de longitud de arco  de esa parte de la curva en el subintervalo correspondiente
de esa parte de la curva en el subintervalo correspondiente ![Rendered by QuickLaTeX.com [x_{i}, x_{i+1}]](https://www.aprendematematicas.org.mx/wp-content/ql-cache/quicklatex.com-cbd37cc99e71e648230c9dc07249ec9b_l3.png) .
.
- 8. Para simplificar esta expresión, observe que
 , implica que
, implica que  , y por el método de Euler,
, y por el método de Euler,  . Entonces,
. Entonces, - 9. Sume el valor aproximado de la longitud
 de cada elemento correspondiente a todos los sub-intervalos.
de cada elemento correspondiente a todos los sub-intervalos. - 10. Evalúe la suma numéricamente.
Observe que a medida que se incrementa ![]() (el número de partes en las que se ha dividido el intervalo
(el número de partes en las que se ha dividido el intervalo ![]() ) cada segmento de línea está más cerca de la parte correspondiente de la gráfica de la función por lo que la aproximación obtenida de
) cada segmento de línea está más cerca de la parte correspondiente de la gráfica de la función por lo que la aproximación obtenida de ![]() se acerca a su valor exacto.
se acerca a su valor exacto.
Luego, para calcular el valor exacto de la longitud del arco, en lugar de dividir el intervalo en un número finito de partes, es necesario dividirlo en una cantidad infinitamente grande de partes, de modo que cada subintervalo sea infinitamente pequeño.

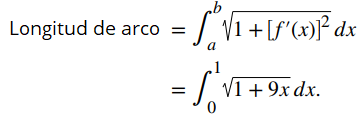


^2} \\ \Delta L_{i} &\approx & \sqrt{1 + (f'(x_i))^2}\cdot \Delta x \end{eqnarray*}](https://www.aprendematematicas.org.mx/wp-content/ql-cache/quicklatex.com-b82ae9ac890792bf5ad502c19a36b9d7_l3.png)

Comentarios
Publicar un comentario